/. SLR parser for the grammar E-E+T (1) E-T (2) T-T.F (3) T-F (4) F-(E) (5) F-ID (6)./ /. Stack structure and fuctions./ /. The only thing important here is that the value associated with each name of the macro should be unique. They have no realtion to the states in. Program to Construct LL (1) Parsing Table in c. LL (1) Parser is Top-Down Parser. It deals with a class of grammar called LL (1). The first ‘L’ denotes the input is scanned from left to right, second ‘L’ denotes leftmost derivation of input and ‘1’ denotes the number of.

The user may build a SLR(1) parse table for a grammar with this operator. As with LL(1) table building, a full discussion of the method of building an SLR(1) parse table is beyond the scope of this discussion. The procedure followed is more or less the same as the SLR parse table building in the Dragon compiler book.

This shares some similarities with the LL(1) parse table builder view. The similarities include the building of the first and follow sets, the operations of controls at the top of the help window and so forth. That may be helpful as a reference.

Slr Parsing Table Program In Ct

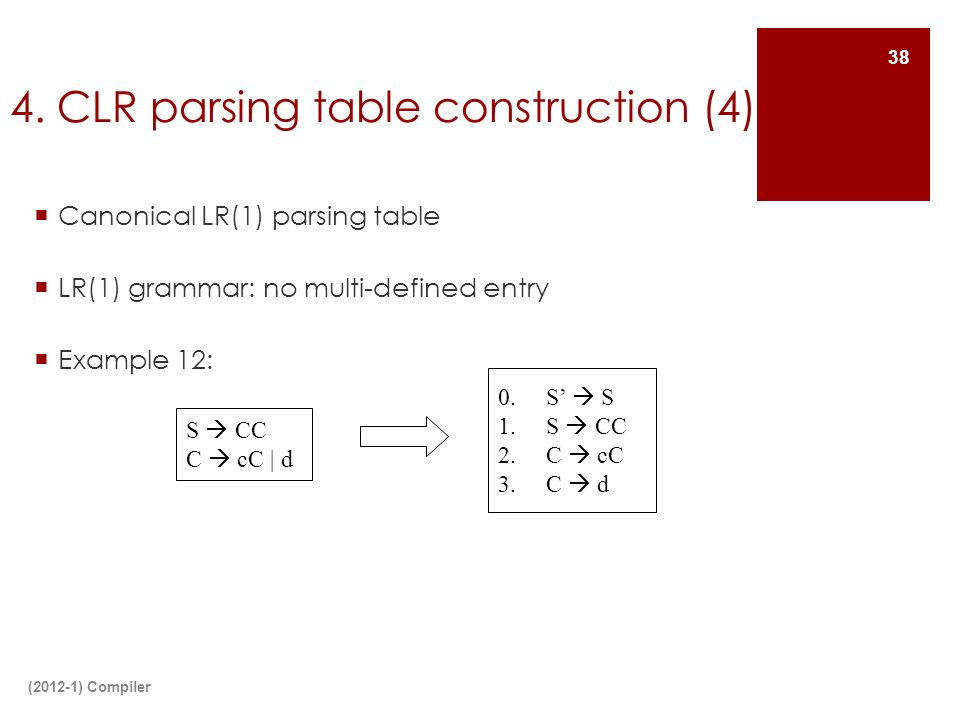
NB: In this view, you may resize the views to see things better. For example, dragging the bar between the sets of items diagram and the parse table will adjust the sizes of both.

Steps

The following steps are completed in order to build an SLR(1) parse table:

1. The user first enters the first and follow sets for each variable. The interaction that takes place here is identical to that of the LL(1) parse table's first and follow sets construction.
2. 
   A set of items construction.

   The next step is the construction of the sets of items in a transitional diagram. What a transitional diagram is and how it is put together is not covered here, as a full description would be prohibitively long. JFLAP represents a transitional diagram by a FSA as shown in the figure at the top of the page, with each state corresponding to a set of items. The initial set of items corresponds to the initial state, and final states represent terminating sets of items. The items in a set are shown in the label below a state.

   An item is essentially a production with some placeholder character; JFLAP uses an underscore, _, as this special character. A production A BCD can produce the four items A _BCD, A B_CD, A BC_D, and A BCD_. The marker _ in an item represents which symbols have been processed (to the left of the marker) and which have not been processed (to the right of the marker).

   During the first part of the sets of items construction, the initial set of items is put together (i.e., S' S and its closure). To expand that set, use the transition tool (), and drag from a set to an empty space in the diagram. The user is queried as to the symbol to expand the set of items on. Once the user enters a grammar symbol and JFLAP confirms that the set of items does goto on that set, a dialog then pops up allowing the user to define the set of items.

   The view used for defining a set of items is shown above. The left hand column lists those productions in the grammar. The right hand column lists items already part of the set. To add an item to the set, click a production in the left hand list. A pop-up menu will appear with all possible placements of the sets of items. To save time, the 'Closure' item will take whatever items are selected in the right column, and add all items which comprise the closure of the selected item. The 'Finish' button will add all items that should be in the set of items. When 'OK' is pressed, the answer will be checked for mistakes. If everything is fine, a new set of items will appear at the point in the empty space that the user initially dragged to.

   If the user wishes to define a transition from an existing set of items to another existing set of items, in creating the transition she may drag to the second set rather than to empty space. This will avoid the bother of defining the second set of items, as JFLAP will assume the set dragged to is that second set.

   One uses the attribute tool () to drag states around, and set final and initial states as per the usual practice when editing. The attribute tool here does not have the ability to change transitions or set labels.

3. Once all sets of items are constructed, the parse table is built. In the parse table, a blank entry indicates an error in parsing, s means shift, r means reduce, a single number means goto that item, and acc is accept. To change the content of a cell, click the cell and start typing. For reduction, the number following the r is a production number. The productions are indexed from 0 onward in the order shown in the list on the left. For example, in the grammar given above r1 means 'reduce by S aSb.' To determine the number of a production without counting, hold the mouse over the production, and a tool tip will appear with the production number. When the table is completed the user may press 'Next.' If there are no errors, one may proceed to parse strings with that table.

Slr Parsing Table Program In Chicago

Help

The style of help that is available for SLR(1) table construction is nearly identical to that available for LL(1) table construction: 'Do Selected,' 'Do Step,' and 'Do All' are all there and work in the same fashion.

In the case of the sets of items construction, the help options available are 'Do Step' and 'Do All,' which will randomly place any set of items. After the items are placed, one may rearrange them to make the view more aesthetically pleasing, but it will otherwise be immutable.

Parsing Details

The top figure shows a completed SLR(1) parse table. Once the table is completed, the user has the option to proceed to parsing strings using the table by pressing the 'Parse' button. The interface for that parsing is explained here.

There may be at least one cell in the table with more than one rule, and the user may choose which of the rules to use before parsing. Cells with more than one expansion are highlighted in a sort of sherbet orange color. One may click on these cells, and a pop-up menu will appear allowing the user to select which expansion to use for this cell. Note that if clarifying ambiguity becomes necessary, the parse table may not accept the same language as the original grammar since, obviously, the parser will not be aware that alternate shifts/reductions/whatever exist.

Sample Program In C++ Programming